Funciones Trigonométricas

Funciones trigonométricas

Funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.

 El nombre de los lados de este triángulo rectángulo son:

• Hipotenusa (c) es el lado opuesto al ángulo recto, o el lado más grande.
• Cateto opuesto (a) es el lado opuesto al ángulo 
• Cateto adyacente (b) es el lado adyacente al ángulo .

Existen seis funciones trigonométricas básicas:

Función
Seno		${\displaystyle \operatorname {sen} \;\theta \equiv {\frac {1}{\csc \theta }}\equiv \cos \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\cos \theta }{\cot \theta }}\,}$
Coseno		${\displaystyle \cos \theta \equiv {\frac {1}{\sec \theta }}\equiv \operatorname {sen} \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\operatorname {sen} \theta }{\tan \theta }}\,}$
Tangente		${\displaystyle \tan \theta \equiv {\frac {1}{\cot \theta }}\equiv \cot \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\operatorname {sen} \theta }{\cos \theta }}\,}$
Cotangente		${\displaystyle \cot \theta \equiv {\frac {1}{\tan \theta }}\equiv \tan \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\cos \theta }{\operatorname {sen} \theta }}\,}$
Secante		${\displaystyle \sec \theta \equiv {\frac {1}{\cos \theta }}\equiv \csc \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\tan \theta }{\operatorname {sen} \theta }}\,}$
Cosecante		${\displaystyle \csc \theta \equiv {\frac {1}{\operatorname {sen} \theta }}\equiv \sec \left({\frac {\pi }{2}}-\theta \right)\equiv {\frac {\cot \theta }{\cos \theta }}\,}$

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa.

Ésta se usa cuando en un triángulo rectángulo se conoce un ángulo agudo y el cateto opuesto, o un ángulo agudo y la hipotenusa, o el cateto  opuesto al ángulo dado:

sen  = opuesto/hipotenusa

2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa.

Si en un triángulo rectángulo conocemos un ángulo agudo y el cateto adyacente, o un ángulo agudo y la hipotenusa :

cos  = adyacente/hipotenusa

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente.

Si en un triángulo rectángulo conocemos un cateto y el ángulo adyacente a él podemos calcular el otro cateto :

tan  = opuesto/adyacente

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto.

Si conocemos un cateto y su ángulo opuesto podemos calcular el valor :

cot  = adyacente/opuesto

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente.

Ésta se usa cuando se tiene lo contrario que en la función coseno:

sec  = hipotenusa/adyacente

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto.

 Ésta se usa cuando se tiene lo contrario a la función seno :

csc  = hipotenusa/opuesto

Signos de las razones trigonométricas por cuadrantes

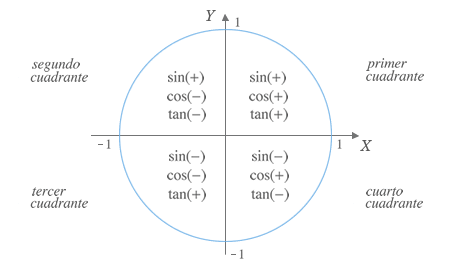
α	0º	90º	180º	270º
sen	0	1	0	−1
cos	1	0	−1	0
tg	0	∞	0	−∞
cosec	∞	1	∞	−1
sec	1	∞	−1	∞
cotg	∞	1	∞	0

Dado que el seno y el coseno de cualquier ángulo α corresponden respectivamente con los valores y y x de la circunferencia goniométrica, sólo pueden tomar valores entre -1 y 1.

Para determinar las razones trigonométricas de cualquier tipo de ángulo utilizaremos una circunferencia goniométrica.

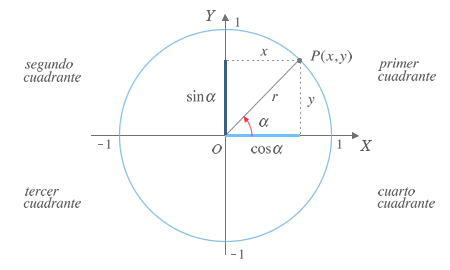
Circunferencia goniométrica

Circunferencia cuyo radio es la unidad y se encuentra centrada en el origen de un sistema de coordenadas. A cada uno de sus puntos P(x,y) les corresponden un único angulo α definido entre el semieje positivo de las abcisas y el segmento OP. Su intersección con los ejes de coordenas la divide en cuatro partes denominadas cuadrantes.

:

sin α=yr=y     cos α=xr=x

Razones	Razones inversas
sin α=y	csc α=1y
cos α=x	sec α = 1x
tg α=yx	cotg α= xy

Referencias:

• Casillas M.. (2014). Qué son las funciones trigonométricas. 14 de marzo del 2019, de matematicasmodernas.com Sitio web: https://matematicasmodernas.com/que-son-las-funciones-trigonometricas/
• Inés J.. (s/f). Gráfica de las funciones trigonométricas. 14 de marzo del 2019, de www.uaeh.edu.mx Sitio web: https://www.uaeh.edu.mx/scige/boletin/prepa3/n1/m10.html
• www.fisicalab.com. (s/f). Razones trigonométricas de cualquier ángulo. 14 de marzo del 2019, de www.fisicalab.com Sitio web: https://www.fisicalab.com/apartado/razones-trigonometricas-cualquier-angulo#contenidos